
L’origine du terme « conique » ?
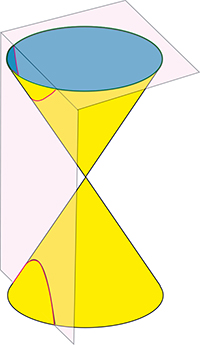
Le terme conique vient de « section conique ». Apollonius de Perge, au IIIe siècle avant notre ère, s’est intéressé à l’intersection d’un cône et d’un plan ne passant pas par son sommet. Le terme de « sections coniques » pour désigner ces courbes s’est depuis simplifié en « coniques ».
Nous en observons tous les jours, sous la forme des taches de lumière que projette une lampe munie d’un abat-jour sur un mur ou sur le sol. Selon que le plan rencontre les deux nappes du cône ou une seule, on obtient une hyperbole ou une ellipse et, dans le cas intermédiaire, une parabole.
Les coniques se distinguent donc selon qu’elles sont bornées (ellipses), non bornées à une seule branche (paraboles) ou à deux branches (hyperboles). Ellipses et hyperboles ont un centre de symétrie. Pour cette raison, elles sont appelées coniques à centre. Elles ont également deux axes de symétrie orthogonaux entre eux, alors que la parabole n’en a qu’un.
À la source des ellipses, paraboles et hyperboles
Ces trois termes viennent également d’Apollonius de Perge, et donc du grec. Comme en linguistique, une ellipse désigne une omission, un manque. Ainsi, en géométrie, il s’agit d’un « cercle ...
Lire la suite
