En général, une situation de la vie ou une expérience de physique ne se décrivent pas à l'aide d'un seul paramètre, mais de plusieurs. La notion de variations dans un tel contexte à plusieurs dimensions doit donc être approfondie. C'est ce que réalisent les dérivées partielles.

Le physicien tâche souvent de minimiser une énergie, l’économiste un coût, l’ingénieur une qualité et le marchand un chiffre d’affaires. Toutes ces situations ont en général en commun de se décrire par une fonction réelle de plusieurs variables, qu’il s’agit d’optimiser. Il s’agit d’une fonction  f qui, pour chaque valeur d’un ensemble de paramètres x1, x 2, x 3… x n , renvoie un nombre noté  f (x1, x 2, x 3… x n ) qui correspond à ce qu’il s’agit d’optimiser. Tout l’enjeu est alors de déterminer les valeurs des paramètres pour lesquelles  f (x1, x 2, x 3… x n ) est minimale (ou maximale, selon le contexte).

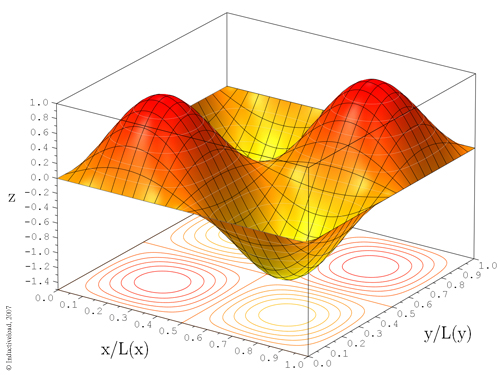
Graphe représentatif d’une fonction de n = 2 variables.

 

Un problème universel

Posée de façon aussi générale, une telle situation est bien trop vaste pour être traitée en totalité. On peut même dire, avec Euler, qu’elle englobe l’entièreté de la réalité du monde, « car puisque la structure de l’univers est la plus parfaite, et qu’elle est l’œuvre d’un très sage Créateur, rien ne s’y passe sans qu’y apparaisse quelque relation de minimum et de maximum ».

Sans entrer dans les détails techniques, on pourra supposer ici que la fonction  f est « suffisamment régulière », c’est-à-dire que son comportement peut se décrire par un ... Lire la suite