

Interview
Dans quel domaine de recherche votre thèse s’inscrit-elle ?
Mon travail se situe à l’interface des mathématiques discrètes et de l’informatique fondamentale. En pratique, cela signifie que j’utilise des techniques issues de la recherche en mathématiques pour répondre à des questions qui relèvent plus de l’informatique théorique (limites théoriques des ordinateurs, algorithmique, logique…).
Ma thèse, intitulée Autour du problème du domino – Structures combinatoires et outils algébriques, a été co-encadrée par Jarkko Kari (Université de Turku, Finlande), Stéphan Thomassé et Nathalie Aubrun (ENS de Lyon, France). Je l’ai en effet effectuée entre l’ENS de Lyon et la Finlande, et je l’ai soutenue le 15 juillet 2020.
Pourquoi avez-vous choisi ce sujet ?
La conjecture de Nivat m’a tout de suite intéressé par sa complexité, malgré son énoncé simple. Elle est également liée au domaine des pavages (par exemple au problème du domino, que l’on retrouve dans le titre de ma thèse), auquel je m’intéresse depuis mon premier stage en laboratoire de recherche.
[Le problème du domino est le suivant (voir Tangente 198, article « Éblouissants pavages de Penrose »). On se donne un ensemble fini de tuiles. La question est de savoir s’il est possible de paver le plan à l’aide de copies de ces tuiles. Le problème a été prouvé comme étant indécidable en 1966 par le mathématicien américain Robert Berger.]
Que peut-on savoir d’une image si l’on ne peut en voir qu’un tout petit morceau à la fois ? Une image numérique est généralement représentée par un tableau de pixels possédant chacun une couleur. Pour être sûr que l’image est assez grande, on l’imaginera ici infinie. Il semble alors étonnant de pouvoir déduire quoi que ce soit sur cette image infinie en n’en voyant qu’une partie finie à la fois. Pourtant, la conjecture de Nivat affirme qu’il est possible de prévoir que cette image se répète si elle ne contient pas un trop grand nombre de « petits morceaux » différents.
Un petit détour linéaire
Avant de s’intéresser au cas d’une image infinie (de dimension 2), il peut être intéressant de s’intéresser au cas d’une ligne infinie (de dimension 1). Considérons donc un ensemble (ou alphabet) fini A de couleurs (ou de lettres), que l’on utilise pour colorier toutes les cases d’une ligne infinie. Une telle ligne est appelée périodique et de période m si, lorsqu’on la translate de m cases, on retombe sur la même ligne : elle se répète indéfiniment.
Imaginons que l’on ne puisse observer cette ligne qu’à travers une fenêtre de largeur fixée n. Le nombre de motifs de taille n apparaissant dans la ligne est appelé la complexité de la ligne ; on la note P(n).

Exemple de coloriage d’une ligne infinie.
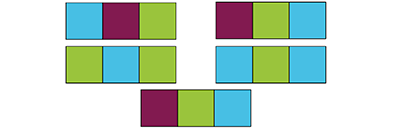
On dénombre en tout cinq motifs de taille 3, et donc P(3) = 5.
Si une ligne est périodique de période n, alors P(n) ≤ n. Les mathématiciens américains Harold Calvin Marston Morse (1892-1977) et Gustav Arnold Hedlund (1904-1993) ont prouvé en 1938 qu’il s’agit en fait d’une caractérisation de la périodicité : une ligne est périodique si, et seulement si, il existe un entier n tel que P(n) ≤ n. La preuve du théorème de Morse-Hedlund est assez élémentaire et permet de revisiter un classique : le raisonnement par récurrence (voir encadré).

Exemple de coloriage périodique d’une ligne.

Motifs de taille 3 : on a P(3) = 3. Ensuite, pour tout n supérieur à 3, on a P(n ) = 3.
La preuve du théorème de Morse–Hedlund
Soit w un mot quelconque, c’est-à-dire une suite (indexée sur l’ensemble des entiers relatifs) de lettres prises dans l’alphabet A. On a déjà P (n + 1) ≤ P (n). En effet, tout motif de taille n+1 commence par un motif de taille n, donc il y a au moins P(n) motifs de taille n + 1.
S’il existe n tel que P (n + 1) = P(n), cela signifie qu’il y a autant de mots de taille n que de mots de taille n + 1. Ainsi, chaque mot de taille n se prolonge de manière unique en un mot de taille n + 1.
De plus, puisqu’il existe P (n) différents motifs de taille n, on sait qu’il existe deux motifs de w espacés de m lettres qui sont égaux, avec m ≤ P (n). Autrement dit, il existe un entier i tel que :
wi + 1 … wi + n = wi + 1 + m … wi + 1 + m + n .
À partir de cette relation, on peut prouver que pour tout entier relatif r on a
wi + r = wi + m + r . En effet, cette égalité est vraie, déjà, pour r compris entre 1 et n. Ensuite, par récurrence sur r, on prouve que c’est le cas pour r supérieur à n. Supposons que c’est le cas pour un r fixé. Alors notre égalité est vraie pour r + 1 aussi, puisque tout motif de taille n se prolonge de manière unique en un motif de taille n + 1. Or, wi + k = wi + m + k pour k compris entre 1 et r et r supérieur à n : les mots
wi + 1…wi + n et wi + 1 + m …wi + 1 + m + n ont les mêmes n dernières lettres, donc ils se prolongent de la même manière. D’où wi + r + 1 = wi + m + r + 1 et la récurrence est prouvée.
On montre de la même manière que l’égalité est vraie pour r négatif.
Or, cette égalité nous dit exactement que w est périodique de période m : on a prouvé que s’il existe n tel que P (n + 1) = P (n), alors w est périodique.
Supposons maintenant que w n’est pas périodique. D’après ce qui précède, P (n + 1) > P (n) pour tout n. Par récurrence sur n, prouvons que P (n + 1) ≥ n + 1 pour n supérieur à 1.
On a P (1) ≥ 2 puisque pour que w ne soit pas périodique il est nécessaire qu’il soit constitué d’au moins deux lettres différentes.
Ensuite, par récurrence, on suppose que pour n fixé, on a P (n) ≥ n + 1. D’après ce qui précède, P (n + 1) > P (n), donc P (n) ≥ P (n) + 1. Et, avec l’hypothèse de récurrence, on en déduit que P (n + 1) ≥ n + 1 + 1 = n + 2, et la récurrence est prouvée.
En prenant la contraposée, et en utilisant le fait que tout mot périodique a une complexité telle que P (n) ≤ n, on obtient bien le théorème de Morse-Hedlund.
En deux dimensions
Revenons à notre image initiale. Au lieu d’une ligne, on a maintenant une grille infinie, toujours coloriée à l’aide d’un certain alphabet fini A ; on appelle un tel coloriage une configuration. On parle maintenant de périodicité selon un vecteur (et non plus un simple nombre) lorsque la configuration est égale au translaté d’elle-même selon le vecteur
.
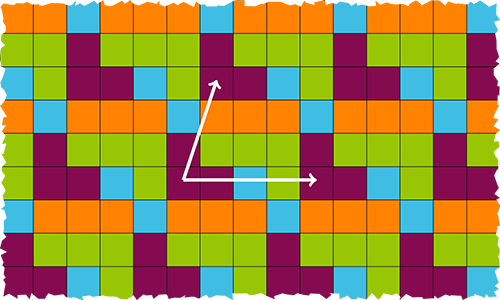
Une configuration périodique selon (1, 3) et (4, 0).
Un motif est maintenant une portion rectangulaire d’une configuration de taille m × n, et la complexité d’une configuration est le nombre de tels rectangles différents que l’on peut y observer à travers cette « fenêtre » de taille m × n. La complexité est notée P (m, n). Comme dans le cas de la ligne, on aimerait obtenir une caractérisation de la périodicité d’une configuration en fonction de sa complexité. L’analogue de la condition P (n) ≤ n serait P (m, n) ≤ mn, puisque mn représente l’aire du rectangle observé.
Malheureusement, il est impossible d’obtenir une caractérisation similaire à celle de Morse et Hedlund : il existe par exemple une configuration périodique ayant une complexité P (m, n) = 2 m + n + 1.
L’autre sens de la caractérisation est l’objet d’une conjecture, formulée en 1997 par Maurice Nivat (1937-2017) et qui porte maintenant son nom : toute configuration telle qu’il existe deux entiers m et n pour lesquels P(m, n) ≤ mn, dite de faible complexité, doit être périodique. Cette borne est en outre optimale, puisqu’il existe des configurations non périodiques de complexité mn + 1.

Toute fenêtre de taille mn laisse apparaître mn motifs différents avec une cellule noire (dans chaque cellule du rectangle), plus un motif entièrement blanc, d’où une complexité mn + 1. La configuration n’est pas périodique : toute translation déplace la cellule noire à une position différente.
Et en dimension 3 ?
Un énoncé similaire au théorème de Morse-Hedlund est vrai en dimension 1 et conjecturé en dimension 2. Et en dimension 3 ? C’est faux !
En 3D, une configuration est de faible complexité par rapport à un parallélépipède de taille mnk si sa complexité P (m, n, k) est inférieure ou égale à mnk. Il est alors possible de construire une configuration 3D de faible complexité qui n’est pas périodique : fixons un entier n et considérons la configuration entièrement blanche, sauf deux lignes infinies perpendiculaires et espacées de n cellules.
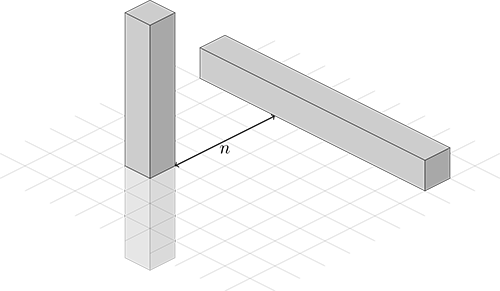
Pour commencer, elle n’est pas périodique, puisque toute translation déplacera au moins une des deux lignes. De plus, sa complexité par rapport à un cube de côté n est P (n, n, n) = 2n 2 + 1 puisque le cube intersecte au plus une ligne. Pour n ≥ 3, on aura bien P(n, n, n) < n 3, donc une configuration de faible complexité.
L’algèbre des polynômes à la rescousse
La preuve complète de la conjecture de Nivat résiste encore aux assauts des mathématiciens. Comme souvent, des avancées considérables ont été concrétisées lorsque ce problème a été relié à un autre domaine a priori sans rapport : l’algèbre polynomiale. Ce lien, aussi surprenant que fructueux, a été mis en évidence par Jarkko Kari et Michal Szabados en 2015.
Pour le comprendre, commençons par voir comment un motif fini peut être représenté par un polynôme. La première étape est de considérer un alphabet A constitué de nombres (inclus dans l’ensemble des entiers par exemple). Un motif p est un coloriage (un « étiquetage ») d’un rectangle m × n par des éléments de A ; la couleur (en fait, le nombre) présente à la position (i, j) est notée pi, j. Le polynôme représentant ce motif est alors le polynôme suivant :
On peut maintenant s’intéresser aux motifs d’un point de vue purement algébrique en étudiant ces polynômes !
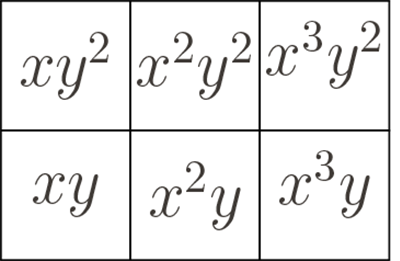
Les positions des différents monômes sur un motif 3 × 2.

Le motif représenté par 3xy + xy 2 + 2x 2 y + 3x 2 y 2 + x 3 y + 2x 2 y 2.
En généralisant cette idée, on peut représenter les configurations comme des « polynômes infinis » (appelés séries formelles), dont les coefficients sont les nombres présents dans les cellules de la configuration. Kari et Szabados ont montré que les polynômes dont le produit avec une série donne 0 sont particulièrement importants ; ils sont appelés polynômes annulateurs (voir encadré).
Pourquoi les polynômes annulateurs ?
Prenons deux configurations c et d, et construisons les séries C et D les représentant :
Avec ce formalisme, on remarque sans aucun calcul que le produit d’une série par un monôme x a y b revient à translater la configuration d’un vecteur (a, b) :
Grâce à cela, il est possible d’obtenir une caractérisation purement algébrique de la périodicité : c est périodique si, et seulement si, il existe deux entiers a et b tels que c est égale au translaté d’elle-même par (a, b), ce qui équivaut à C = x a y b C, ou encore à (x a y b — 1) C = 0.
En résumé, c est périodique si, et seulement si, il existe un polynôme annulateur de la forme x a y b — 1. Étudier les polynômes annulateurs est ainsi un moyen algébrique de prouver qu’une configuration est périodique.
Mieux : l’ensemble des polynômes annulateurs d’une configuration est un idéal polynomial, un objet mathématique dont la structure est relativement bien connue.
En comprenant mieux à quoi peuvent ressembler les polynômes annulateurs, Kari et Szabados parviennent à montrer plusieurs résultats nouveaux.
Pour commencer, toute configuration c de faible complexité peut s’écrire comme une somme de configurations périodiques c1, c2… cr , qui peuvent cependant avoir un alphabet infini : c = c1 + c2 +… + cr .
Ils parviennent également à prouver une version asymptotique de la conjecture de Nivat : si P(m, n) ≤ mn pour une infinité d’entiers m et n, alors la configuration est périodique.
Enfin, en mêlant leur approche algébrique avec des outils développés par Van Cyr et Bryna Kra, ils parviennent à montrer que si une configuration est somme de seulement deux configurations périodiques, alors elle vérifie la conjecture de Nivat.
Dans la thèse Autour du problème du domino – Structures combinatoires et outils algébriques, ces outils algébriques sont encore développés pour obtenir de nouveaux résultats se rapprochant de la conjecture de Nivat. Une partie du travail s’est concentrée sur les configurations uniformément récurrentes, c’est-à-dire celles qui ne contiennent pas de motifs isolés.
Éliminer les directions problématiques
Les techniques développées par Cyr et Kra reposent sur la notion de déterminisme d’un ensemble X de configurations. X est dit déterministe dans une direction si, lorsque deux configurations de X sont égales sur un demi-plan dans cette direction, alors elles sont égales partout.
Autrement dit, la valeur que prennent les configurations sur un demi-plan dans la direction détermine la valeur des configurations tout entières.

Un demi-plan de direction 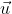 = ( – 1,2 ). S’il existe au plus une configuration de X avec une valeur donnée sur ce demi-plan, alors X est déterministe dans la direction
= ( – 1,2 ). S’il existe au plus une configuration de X avec une valeur donnée sur ce demi-plan, alors X est déterministe dans la direction 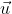 .
.

Maurice Paul Nivat (1937– 2017).
Toute direction est donc soit déterministe, soit non déterministe. Le dernier cas encore ouvert après les travaux de Cyr et Kra est celui des directions pour lesquelles X est déterministe selon
mais non déterministe selon
. L’un des résultats les plus importants de la thèse montre que, dans le cas des configurations uniformément récurrentes, ces directions problématiques peuvent en fait être « éliminées ». Cela permet de prouver que la conjecture de Nivat est vraie pour les configurations uniformément récurrentes.
Uniformément quoi ?
À partir d’une configuration c, il est possible de construire son orbite O (c), qui contient les translations de c par tout vecteur de
. Ensuite, en prenant la clôture
de l’orbite, on obtient un ensemble contenant toutes les translations de c, ainsi que les configurations limites par ces translations. Une configuration est uniformément récurrente si, pour toute configuration c’ dans
, on a
Autrement dit, on ne peut pas « effacer » de motifs de c en en faisant une translation, même infinie.
Le résultat précis obtenu dans la thèse avec Jarkko Kari montre que, pour toute configuration de faible complexité, contient une configuration périodique d. Notez que si la conjecture de Nivat est vraie, alors toute configuration de
est périodique.
Puisque d est périodique, ne contient que des configurations périodiques. Or, c étant uniformément récurrente,
donc toutes les configurations de
sont périodiques, y compris c elle-même.
La dernière chose à faire pour prouver la conjecture de Nivat est donc d’étudier le cas des configurations non uniformément récurrentes. Mais elles restent encore mal comprises, rendant la conjecture encore inaccessible pour le moment.
