Si le plan est colorié à l’aide de deux couleurs, il est facile de montrer que, quel que soit l’entier strictement positif d, alors on peut trouver deux points de la même couleur espacés de d. Il suffit en effet de considérer les trois sommets d’un triangle équilatéral de côté d pour s’en convaincre.
Maintenant, qu’en est-il si le plan est colorié avec plus de deux couleurs ?
Le plan tricolore
Les points d’un plan sont tous affectés d’une couleur, de façon aléatoire : bleu, blanc et rouge par exemple. Peut-on affirmer qu’il existera un segment de longueur d cm dont les extrémités sont de la même couleur ?
La réponse est affirmative et la preuve repose sur une figure particulière, la navette (ou le fuseau) de Moser (en anglais, Moser spindle). Cette construction est due aux deux frères et mathématiciens canadiens Léo Moser (1921–1970) et William Oscar Jules Moser (1927–2009).
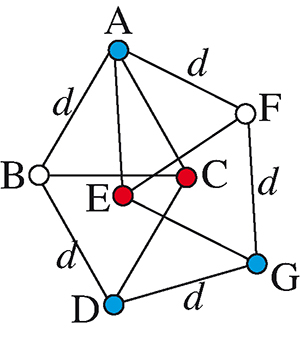
Cette figure est formée de deux losanges, eux-mêmes constitués de deux triangles équilatéraux de côté d cm. Raisonnons par l’absurde, en supposant qu’il n’existe pas un tel segment dont les extrémités soient de la même couleur. Alors, si les sommets sont colorés à l’aide des trois couleurs, on aboutit à deux sommets D et G de la même couleur et distants de d cm, c’est-à-dire à une contradiction. On en déduit l’existence d’un segment de d cm dont les extrémités sont de la même couleur, dans tout plan colorié à l’aide de trois couleurs.
Voici le problème posé dans les années 1950 par le mathématicien suisse Hugo Hadwiger (1908–1981) et le mathématicien américain Edward Nelson (1932–2014) : quel est le nombre chromatique du plan, c’est-à-dire le nombre minimal de couleurs nécessaires pour colorier le plan de telle sorte que deux points quelconques distants d’une unité ne soient jamais de la même couleur ? Jusqu’en 2018, on ne savait pas si la réponse à ce problème était 4, 5, 6 ou 7.
En 2018, le mathématicien amateur britannique Aubrey de Grey a construit un graphe G à 1 581 sommets, de nombre chromatique 5 (c’est-à-dire tel que quatre couleurs ne permettent pas d’éviter que deux sommets de G distants d’une unité ne soient de la même couleur). La preuve a dû en être faite et vérifiée par ordinateur ; des graphes « plus petits » ont été obtenus depuis (le record comporte 510 sommets).

Aubrey David Nicholas Jasper de Grey (né en 1963) vient de se voir décerner
le prix David P. Robbins, attribué tous les trois ans
par la Mathematical Association of America,
pour avoir prouvé que le nombre chromatique du plan est au moins égal à 5.
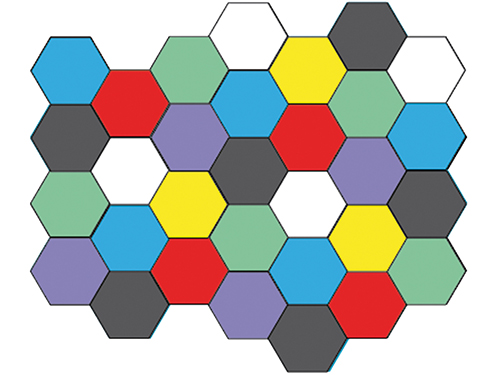
En revanche, on peut colorier le plan à l’aide de sept couleurs différentes de façon que deux points distants de 1 cm ne soient jamais de la même couleur. Pour obtenir un tel coloriage, il suffit de colorier convenablement, à l’aide de sept couleurs, un pavage du plan obtenu à partir d’hexagones réguliers de côté strictement compris entre (environ 0,378) et 1 / 2.
Pourquoi les côtés des hexagones doivent-il être strictement supérieurs à ?