
Le graphe est une notion essentielle en mathématiques. Ici, on s’intéressera à des graphes formés d’un nombre fini de sommets, chacun relié à d’autres sommets par une ou plusieurs arêtes. Ces dernières peuvent éventuellement être orientées.
Un graphe peut représenter par exemple un réseau de communication (comme le réseau de tramway de la ville de Zürich, ou le réseau de métro parisien), le réseau neuronal d’un animal (tel que le système nerveux du vers Caenorhabditis Elegans, le seul animal pour lequel ce réseau est explicitement et complètement connu), ou encore un arbre généalogique (voir les Graphes, Bibliothèque Tangente 54, 2015).
Pour le type de question et d’applications qui nous intéressent le plus, les arêtes des graphes qui apparaissent seront supposées sans orientation.
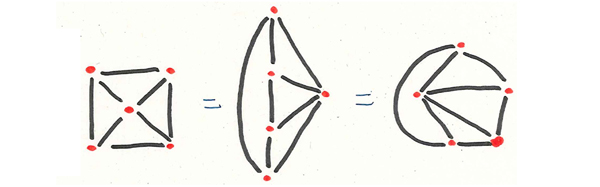
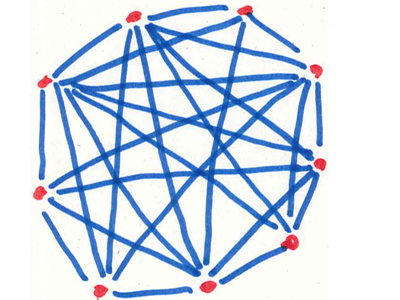
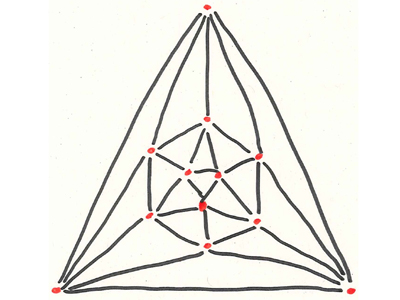
Trois représentations d’un même graphe G possédant cinq sommets et huit arêtes.
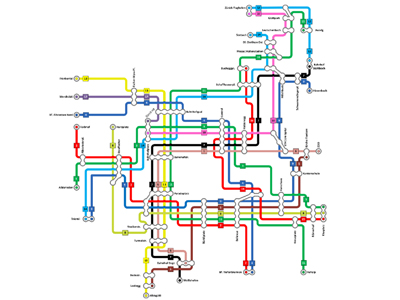
Le réseau de tramway de Zürich.
L’expansion dans les graphes
Des graphes particuliers, qualifiés d’expanseurs, possèdent des propriétés si remarquables que leur existence même semble paradoxale. De fait, plus d’un mathématicien semble avoir d’abord pensé qu’ils ne pouvaient pas exister ! En outre, ils ont des applications extraordinaires dans des domaines très variés des mathématiques et de l’informatique (combinatoire, géométrie, arithmétique, théorie des nœuds…).
L’histoire des graphes expanseurs est entièrement moderne puisqu’elle débute à la fin des années 1960. Elle démontre de manière éclatante l’unité de la mathématique. Même aujourd’hui, à une époque où la recherche est de plus en plus spécialisée et souvent conceptuellement difficile, il est possible que de nouvelles idées révolutionnaires apparaissent qui soient élémentaires, et accessibles à un large public.
Intuitivement, un graphe expanseur combine deux propriétés qui semblent contradictoires : d’une part, il est possible de naviguer très efficacement pour relier deux sommets quelconques, même si de nombreuses arêtes du graphe venaient à disparaître soudainement ; d’autre part, le « coût » du réseau n’est pas démesuré, à savoir que le nombre d’arêtes est relativement « petit » par rapport au nombre de sommets (il ne s’agit donc pas de simplement relier tous les sommets entre eux !). Plus précisément, on peut associer à un graphe G une certaine constante h(G) positive, appelée le nombre de Cheeger de G (voir en encadré). Si h(G) > 0, cela signifie que le graphe est connexe : il est toujours possible de relier n’importe quelle paire de sommets en suivant des arêtes du graphe. Mais plus h(G) est grand, et plus le graphe est « robuste » : par exemple, si h(G) vaut au moins 1/10, alors on peut toujours relier deux parties de taille similaire du graphe, même après avoir enlevé une arête sur dix dans le graphe !
Le nombre de Cheeger
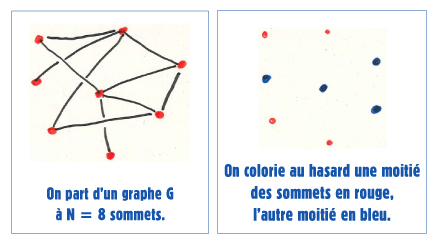
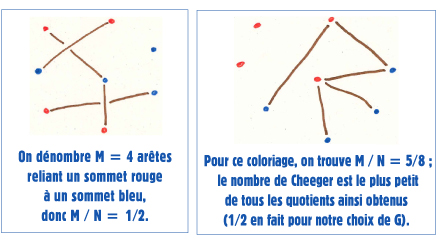
On note N le nombre de sommets du graphe. Partageons l’ensemble des sommets en deux parties de taille N/2 (environ), disons A et B. La constante de Cheeger du partage (A, B) est le quotient M/N, où M est le nombre d’arêtes du graphe dont une extrémité est dans A et l’autre dans B. Le nombre de Cheeger est alors le plus petit des quotients M/N obtenu lorsque l’on regarde tous les partages possibles du graphe en deux morceaux.
Par exemple, si le graphe est un long cycle de N sommets, la constante de Cheeger est de l’ordre de 1/N.
Dire que l’on a des graphes expanseurs signifie alors que l’on sait construire, pour un nombre N arbitrairement grand, un graphe ayant au moins N sommets, où chaque sommet est relié, au plus, à un « petit » nombre fixé d’autres sommets (par exemple, à au plus six autres sommets), et où le nombre de Cheeger est toujours au moins 1/10 (ou toute autre valeur fixée strictement positive).
Graphe d’un réseau très efficace mais de coût démesuré :
le nombre d’arêtes est très supérieur au nombre de sommets.

Graphe d’un réseau particulièrement peu efficace :
un seul incident suffit à couper le réseau en deux parties déconnectées.
Une histoire mouvementée
Pendant longtemps, la découverte des graphes expanseurs, et en particulier la preuve de l’existence de ces objets, a été attribuée à Mark Semenovitch Pinsker, au sujet d’un problème d’informatique théorique. Pinsker introduit en effet en 1973 les graphes expanseurs comme objets auxiliaires lui permettant de faire aboutir une certaine construction, et il prouve qu’une suite de graphes de plus en plus grands « prise au hasard », chaque sommet ayant toujours au plus quatre voisins, a la propriété d’être un expanseur. Cependant, beaucoup plus récemment, Larry Guth a (re)découvert un article fascinant de Yanis Barzdin et Andreï Kolmogorov, publié en 1967, quelques années avant celui de Pinsker. On y trouve non seulement une définition essentiellement équivalente à celle des graphes expanseurs (une différence étant que Barzdin et Kolmogorov utilisent des graphes orientés), ainsi que la preuve de leur existence, mais aussi la première application des graphes expanseurs en dehors de la combinatoire et de l’informatique théorique. Cette application est en outre particulièrement élégante.
Premières constructions
L’histoire cependant continue. En effet, tant Barzdin et Kolmogorov que Pinsker démontrent l’existence de graphes expanseurs… sans en fournir d’exemples concrets. Ils affirment seulement que si l’on construit un graphe « sans réfléchir », il a de bonnes chances d’être expanseur. Ce type de construction aléatoire, bien que parfaitement acceptable s’il s’agit de démontrer l’existence de certains objets, peut poser deux types de problèmes.

Andreï Nikolaïevitch Kolmogorov (1903–1987) en 1964.
Déjà, il est possible que, pour une certaine application concrète, il ne soit pas loisible de choisir soi-même les graphes dont on a besoin. Il n’est guère utile de savoir qu’il existe un graphe expanseur si la question est de vérifier qu’un graphe particulier possède une bonne propriété d’expansion.
En outre, il est intellectuellement toujours naturel de se demander si une construction aléatoire peut être remplacée par une version explicite et déterministe.
Dès 1973, Gregori Aleksandrovitch Margulis est parvenu à construire des exemples explicites de graphes expanseurs. Il a utilisé pour cela un argument extrêmement élégant qui faisait le lien entre l’expansion de certains graphes et des notions profondes d’algèbre et de géométrie. Depuis, de nombreuses autres constructions ont été découvertes, mais l’existence des graphes expanseurs garde toujours un côté mystérieux.
Une petite question de géométrie
Parmi les nombreuses applications des graphes expanseurs, deux des plus belles sont directement reliées à l’article original de Barzdin et Kolmogorov. La première était leur motivation, et la seconde, liée à un problème de théorie des noeuds, a été découverte par Mikhaïl Gromov et Larry Guth.
La motivation est décrite ainsi par Barzdin dans les notes aux oeuvres de Kolmogorov :
« Je ne me rappelle pas en quelle occasion Andreï Nikolaïevitch avait mentionné ces résultats pour la première fois (je n’étais pas présent à cette occasion). Je sais seulement que le sujet qui était discuté était d’expliquer le fait que le cerveau (par exemple celui d’un être humain) est construit de manière que sa plus grande partie est occupée par des fibres nerveuses (axones) tandis que les neurones sont seulement placés à la surface. »
De manière plus précise, Barzdin et Kolmogorov considèrent un graphe fini, ayant N sommets, dont chaque sommet possède (disons) au plus six voisins. Un tel graphe peut toujours être représenté dans l’espace de sorte que deux arêtes ne se croisent pas, sauf éventuellement en un sommet commun. Si l’on suppose que les sommets et les arêtes sont représentés « physiquement » par des billes ou des tubes de 1 cm de rayon, la question devient alors :
Quel est le plus petit rayon R > 0 possible pour que l’on puisse représenter le graphe dans l’espace dans un cube de côté R ?

Chaque sommet du graphe est relié au plus à six autres. Comment passer de la manière la plus efficace du schéma du plan au volume dans l’espace ?
Barzdin et Kolmogorov obtiennent deux résultats :
– On peut toujours représenter un graphe dans un cube de côté environ N1/2 ;
– Si le graphe est expanseur (si sa constante de Cheeger est « suffisamment grande »), alors on ne peut pas représenter le graphe dans un cube de côté inférieur à (environ) N1/2.
Ainsi, Barzdin et Kolmogorov démontrent en quelque sorte que les graphes expanseurs sont « aussi compliqués que possible ». Leur preuve est relativement élémentaire, du moment que la définition exacte de la constante de Cheeger est connue (voir en encadré).
L'argument de Barzdin et Kolmogorov
Considérons un cube de côté minimal R contenant le graphe ; coupons-le par un plan P de sorte que la moitié des sommets soient d’un côté du plan, et l’autre moitié de l’autre côté. Que voit-on alors sur le plan ? On observe un petit disque pour chaque arête reliant les deux côtés, et ces arêtes sont distinctes ; leur aire totale ne peut dépasser l’aire de l’intersection du plan et du cube, qui est au plus de l’ordre de R2. Mais si la constante de Cheeger est, disons, strictement supérieure à 1/10, l’aire totale des disques est au moins π N/10, donc R2 > π N/10, ce qui fournit le résultat voulu.
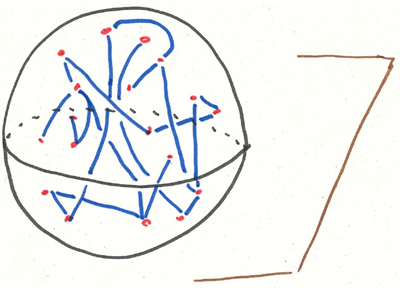
La moitié des sommets du graphe est au-dessus du plan de coupe P, et l’autre moitié en dessous.
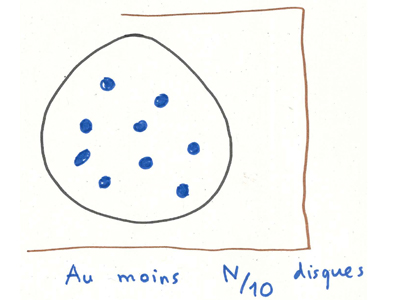
Dans le plan de coupe P, on voit la trace d’au moins N/10 disques d’aire π, correspondant à des arêtes joignant des sommets disposés de chaque côté de P.
Le premier résultat de Barzdin et Kolmogorov était en fait déjà connu de certains informaticiens « appliqués », pour qui il est important de disposer d’un algorithme efficace pour représenter physiquement un réseau dans un espace tri-dimensionnel.
Le second résultat, quant à lui, n’aurait aucun intérêt si les graphes expanseurs n’existaient pas ! C’est donc pour vérifier que leur énoncé n’est pas vide que les deux mathématiciens russes démontrent ensuite l’existence de tels graphes. Par contre, il est également clair qu’il n’est nullement nécessaire ici de construire explicitement ou de disposer d’exemples explicites.
Exemple de graphe expanseur obtenu par la méthode probabiliste. Les N sommets sont fixés.
Chaque sommet est relié à quelques autres sommets choisis au hasard.
Le théorème de Gromov–Guth
La seconde application des graphes expanseurs est particulièrement élégante, en partie parce que l’énoncé du résultat final ne fait absolument pas mention du moindre graphe ! Il s’agit d’une question posée par Gromov dans les années 1980, concernant une manière géométrique de mesurer la complexité des nœuds. Plaçons un tel nœud dans l’espace. Gromov définit la distorsion du nœud par le plus grand quotient A/B, où A est la distance entre deux points du nœud lorsque l’on suit le nœud lui-même, et B est la distance « à vol d’oiseau » entre les deux points.
Maintenant, déplaçons le nœud arbitrairement dans l’espace, en se permettant même de l’étirer arbitrairement. À chaque position est associée une distorsion, et la distorsion intrinsèque du nœud est la plus petite des distorsions possibles lorsque l’on fait prendre au nœud toutes les positions possibles. Si un nœud a une grande distorsion, cela signifie qu’il est extraordinairement compliqué, puisque – quelle que soit la manière dont on le présentera dans l’espace – il y aura des points « proches » à vol d’oiseau qui sont en fait très éloignés le long du nœud.
Comme pour les graphes expanseurs, l’existence de nœuds aussi compliqués n’est pas du tout évidente. Gromov avait effectivement demandé :
Existe-t-il des nœuds de distorsion arbitrairement grande ?
Gromov et Guth, en utilisant les propriétés d’expansion de certains graphes particuliers, parviennent à répondre positivement à la question.
On peut se demander si, étant donné un graphe G explicite, on peut calculer rapidement sa constante de Cheeger h(G), et ainsi vérifier s’il a de bonnes propriétés d’expansion. La définition fournit une méthode de calcul évidente de h(G), mais extraordinairement inefficace : elle nécessite en l’état un nombre d’opérations environ égal à 2N, où N est le nombre de sommets de G. Heureusement, il existe une autre constante associée au graphe, beaucoup plus facile à calculer, qui permet au moins de donner des estimations de la constante de Cheeger h(G). Il reste cependant de nombreuses questions ouvertes relatives à ce domaine en pleine… expansion.
Ce texte est issu de la conférence « Les graphes, un autre univers en expansion » donnée par l'auteur le 20 février 2019 dans le cadre du cycle « Un texte, un mathématicien » à la Bibliothèque Nationale de France.
Emmanuel Kowalski est professeur de mathématiques à l'École polytechnique fédérale de Zürich (Suisse).
