Le Traité du Triangle Arithmétique et traités connexes, dont il existe une première version en latin, a été rédigé par Pascal en 1654 puis publié en 1665. On sait que ce « triangle arithmétique » a été représenté bien avant Pascal, sous une forme ou sous une autre, et son histoire est particulièrement riche et passionnante (voir Tangente 176). On connaît le Pascal penseur, physicien, polémiste, apologiste, et bien sûr mathématicien, mais maintenant on le considère aussi comme philosophe, capable de distinguer connaissances scientifiques et révélation, se montrant rationaliste dans le premier cas, étudiant les textes (la Bible, saint Augustin…) dans le second cas. Dans sa démarche, il mêle observation, induction, déduction et communication de ses découvertes avec un art remarquable. Ainsi, Pascal se veut savant mais aussi écrivain souhaitant être lu et compris par les personnes cultivées.
La recherche de la vérité
Pascal a le souci de transmettre la vérité : « On peut avoir trois principaux objets dans la recherche de la vérité : (1) l’un de la découvrir quand on la cherche ; (2) l’autre de la démontrer quand on la possède ; (3) le dernier, de la discerner d’avec le faux, quand on l’examine. Je ne parle pas du premier : je traite particulièrement le second et il enferme le troisième. »
Pour le Traité, ce sont surtout les deux premiers objets qui sont concernés : il faut découvrir la vérité en examinant le triangle arithmétique, c’est-à-dire deviner des relations vraies ; cela relève de la recherche mathématique. La seconde étape est de les démontrer, c’est-à-dire de construire un raisonnement convaincant et rigoureux. L’objet (3) est aussi concerné, en lien avec l’objet (1), car le chercheur va souvent « tester » des hypothèses, en particulier rechercher d’éventuels contre-exemples prouvant la fausseté de certaines conjectures.
Avant de plonger plus avant dans l’étude du texte, empruntons au mathématicien Pierre Humbert (1891‒1953) la notation suivante : (r, p) désignera le nombre situé dans la case correspondante à la ligne horizontale de rang (parallèle) r et à la ligne verticale de rang (perpendiculaire) p. Ainsi (5, 3) = 15 ou encore (3, 7) = 28. Avec cette notation, la règle de construction du triangle est la suivante : (r, p) = (r – 1, p) + (r, p – 1). Pascal écrit : « Le nombre de chaque cellule est égal à celui de la cellule qui la précède dans son rang perpendiculaire, plus celui de la cellule qui la précède dans son rang parallèle. Ainsi la cellule F, c’est-à-dire le nombre de la cellule F, égale la cellule C, plus la cellule E, et ainsi des autres. »
Les trois premières propositions de Pascal sont :
1. (r, 1) = (1, p) = 1.
2. (r, p) = (r – 1, 1) +… + (r – 1, p).
3. (r, p) = (1, p – 1) + (2, p – 1) +… + (r, p – 1).
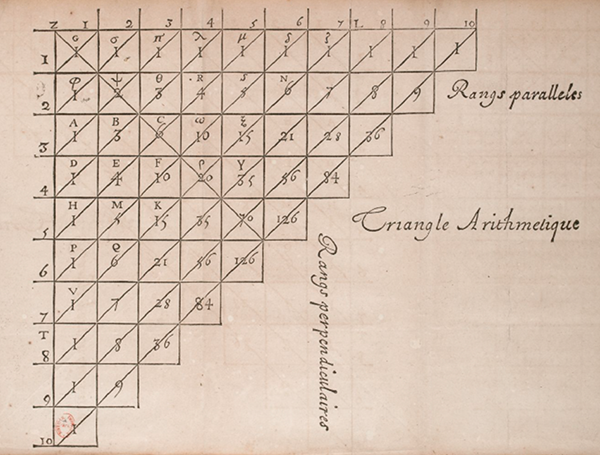
Le triangle de Pascal dans le Traité du triangle arithmétique.
Étudions la preuve de la deuxième proposition. Pascal écrit : « En tout triangle arithmétique, chaque cellule est égale à la somme de toutes celles du rang parallèle précédent comprises depuis son rang perpendiculaire jusqu’au premier inclusivement. » Il choisit une cellule « quelconque » ω ; il affirme qu’elle est égale à R + θ + ψ + φ.
En effet, ω = R + C, mais C = θ + B et B = ψ + A et A = φ, en utilisant la règle de construction du triangle.
Sans le symbolisme algébrique, il semble bien difficile de proposer une démonstration générale, c’est-à-dire en désignant une cellule quelconque par un nouveau symbole.
De plus, le raisonnement par récurrence s’impose puisqu’on travaille sur tous les entiers naturels, ensemble infini de nombres. Il n’en demeure pas moins que la preuve est convaincante et compréhensible même par un novice en mathématiques.
Une preuve rigoureuse de la proposition 2
Soit à prouver que, pour tous entiers p ≥ 1 et r >1, on a l’égalité (r, p) = (r – 1, 1) + (r – 1, 2) +… + (r – 1, p) ; l’utilisation des pointillés pour signifier que p varie de 1 à p est anachronique et n’existe pas du temps de Pascal.
On raisonne par récurrence sur n = p + r, avec r ≥ 2.
Si n = 3, nécessairement r = 2 et p = 1 ; on a bien (2, 1) = (1, 1) = 1.
Si n = 4, on a (3, 1) = (2, 1) = 1 ou (2, 2) = (1, 1) + (1, 2) = 1 + 1 = 2.
On suppose la propriété démontrée jusqu’au nombre n et on considère le couple (r, p) avec r + p = n + 1. On a (r, p) = (r, p – 1) + (r – 1, p) avec r + ( p – 1) = ( r – 1) + p = n. Donc, par hypothèse de récurrence, (r, p) = (r – 1, 1) +… + (r – 1, p – 1) + (r – 1, p).
On constate que le raisonnement par récurrence, sans être trop élaboré, n’est pas des plus évidents : il fait intervenir deux variables, r et p. Un lecteur non initié préférera, au moins dans un premier temps, la démonstration « visuelle » de Pascal à la démonstration rigoureuse, plus satisfaisante intellectuellement mais… guère plus convaincante.
Les propositions suivantes sont :
4. (r, p) –1 = (1, 1) + (1, 2) +… + (1, p–1) + (2, 1) +… + (2, p –1) +… + (r –1, 1) + (r –1, 2) +… + (r –1, p –1).
5. et 6. (r, p) = (p, r).
7. Soit Sq la somme des nombres contenus dans une même base de rang q. On a Sq+1 = 2Sq.
8. Sq = 2q–1.
Démontrons (à la manière de Pascal) la proposition 7., que Pascal énonce ainsi : « En tout Triangle arithmétique, la somme des cellules de chaque base est double de celles de la base précédente. » Pascal choisit une base « quelconque » DBθλ (q = 4) et il montre que la somme des nombres des cellules est le double de la somme des nombres des cellules de la base pour q = 3, à savoir Aψπ.
Les extrêmes D et λ égalent les extrêmes A et π et les deux autres B et θ sont respectivement égales à A + ψ et ψ + π, donc D + B + θ + λ est le double de A + ψ + π. Et Pascal de conclure : « La même chose se démontre de même pour toutes les autres. »
Sans aucun doute, pour un lecteur actuel, la « preuve » est insuffisante, mais à l’époque (et encore bien après) une telle démonstration semblait convaincante.
Par exemple, les démonstrations sur les substitutions (ou permutations) furent souvent explicitées à partir d’exemples.
Seul le raisonnement par récurrence permet d’atteindre la rigueur souhaitable, mais Pascal ne juge pas utile ici de l’utiliser, preuve s’il en est qu’une « démonstration par l’exemple » lui paraît tout à fait suffisante et parfaitement admise par ses lecteurs.
Le recours à la récurrence
Les propositions suivantes du traité sont :
9. Sq – 1 = Sq–1 + Sq–2 +… + S1.
10. « Dans tout triangle arithmétique, la somme de tant de cellules qu’on voudra de sa base, à commencer par une extrémité, est égale à autant de cellules de la base précédente, plus encore autant hormis une. »
11. (r, r) = 2(r – 1, r) = 2(r, r – 1).
12. (r + 1, p – 1)/(r, p) = (p – 1)/r.
Par exemple : (5, 3)/(4, 4) = 3/4 car (5, 3) = 15 et (4, 4) = 20 ; ici, r = 4 et p = 4.
Pascal introduit dans cette douzième proposition une ébauche de raisonnement par récurrence pour démontrer le résultat énoncé ; il écrit : « Quoique cette proposition ait une infinité de cas, j’en donnerai une démonstration bien courte en supposant deux lemmes. »
Le lemme 1 énonce que la proposition est vraie dans la seconde base.
Le lemme 2 énonce que, si cette proposition est vraie dans une base quelconque, alors elle est vraie dans la base suivante. Mais, pour démontrer le second lemme, Pascal utilise une démonstration par l’exemple, ce qui justifie la remarque du mathématicien Hans Freudenthal (1905‒1990) : « Le raisonnement de Pascal est presque un raisonnement par récurrence. »
Pourquoi Pascal juge-t-il nécessaire d’introduire un raisonnement par récurrence ? Ici, il est évident qu’il est impossible de lire sur le triangle le résultat formulé dans la proposition 12. Il serait intéressant d’analyser la démarche de Pascal le menant à cet énoncé : par quelle démarche expérimentale est-il parvenu à cette proposition ?
Les propositions suivantes sont :
13. (r + 1, p) / (r, p) = (p + r – 1) / r.
14. (r, p + 1) / (r, p) = (p + r – 1) / p.
15. [(r, 1) +… + (r, m)] / (r, m) = (m + p – 1) / r (voir l’article « Un orfèvre du raisonnement par récurrence » pour le traitement d’une conséquence de cette proposition).
16.« En tout Triangle arithmétique, un quelconque rang parallèle est au rang inférieur comme l’exposant du rang inférieur à la multitude de ses cellules. »
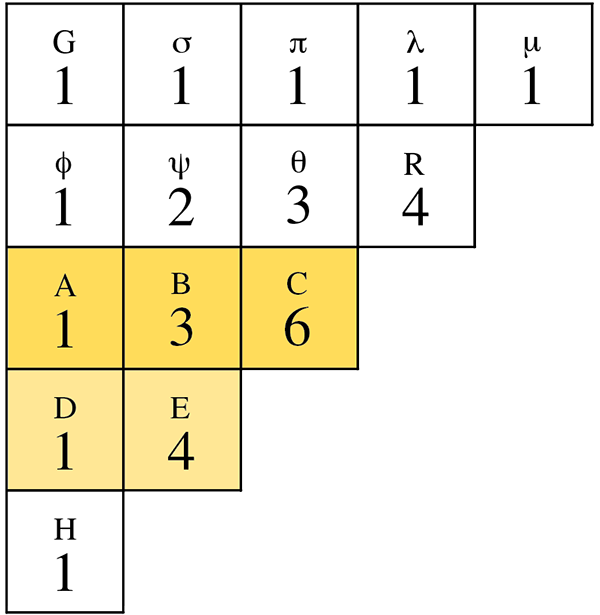
Pascal considère le cinquième triangle, μGH, puis choisit le troisième rang avec pour somme des cellules A + B + C ; le rang inférieur a pour somme D + E et il s’agit de prouver que (A + B + C) / (D + E) = 4/2, où 4 est l’exposant du rang quatrième et 2 le nombre de ses cellules. Mais A + B + C = F, D + E = M et F est à M comme 4 à 2 (proposition 12).
Illustration de la proposition 16.
On a (1 + 3 + 6)/(1 + 4) = 4/2, où, dans cette représentation,
« 4 » est le numéro de la ligne inférieure et « 2 » son nombre de cellules.
17. Soit (r, p) une cellule.
On a [(1, p) +… + (r, p)] / [(r, 1) +… + (r, p)] = r / p.
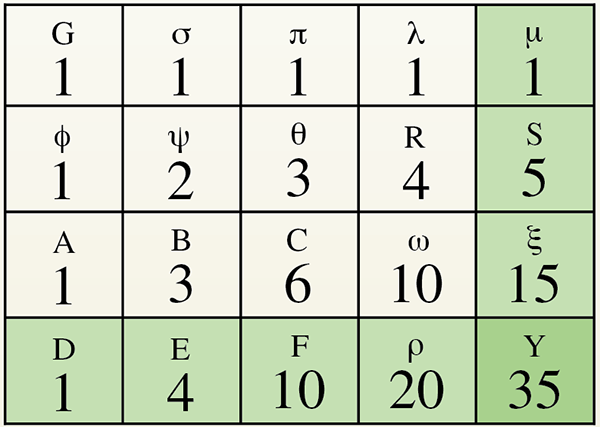
Illustration de la proposition 17.
On a (1 + 5 + 15 + 35)/(1 + 4 + 10 + 20 + 35) = 4/5, où, dans cette représentation,
« 4 » et « 5 » sont les numéros de la ligne et de la colonne considérées.
18.« En tout Triangle arithmétique, deux rangs parallèles également distants des extrémités sont entre eux comme la multitude de leurs cellules. »
Pascal donne comme exemple le triangle GVζ et il considère les rangs P + Q et ϕ + ψ + θ + R + S + N ; P + Q = 7 et ϕ + ψ + θ + R + S + N = 21. On a 7 / 21 = 2 / 6 = 1 / 3.
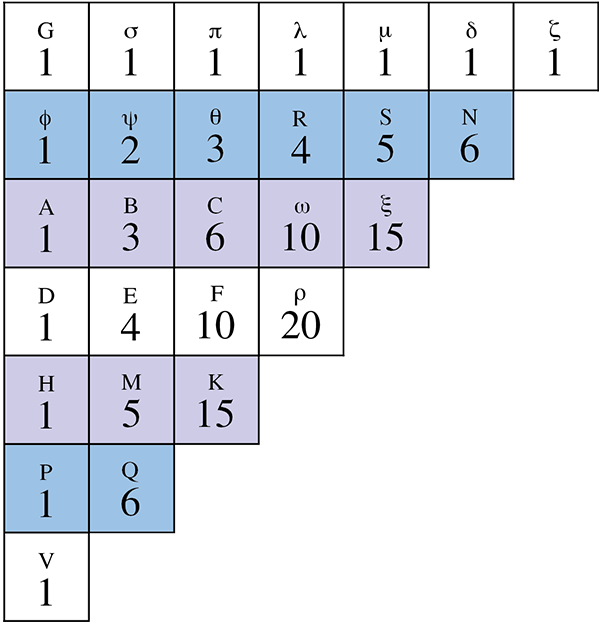
Illustration de la proposition 18.
On a (1 + 6)/(1 + 2 + 3 + 4 + 5 + 6) = 2/6, où, dans cette représentation,
« 2 » et « 6 » sont les nombre de cellules des deux lignes considérées.
On a aussi (1 + 5 + 15)/(1 + 3 + 6 + 10 + 15) = 3/5.
19. « En tout Triangle arithmétique, deux cellules continues dans le dividende, l’inférieure est à la supérieure prise quatre fois, comme l’exposant de la base de cette supérieure à un nombre plus grand d’une unité. »
Cela s’écrit, avec la notation de Humbert, ( p + 1, p + 1) / 4( p, p) = (2p – 1) / 2p.
Les combinaisons et leurs propriétés
Le lecteur moderne est habitué à utiliser les combinaisons :
on note ou encore
le nombre de combinaisons de p objets pris parmi n objets distincts.
Il est facile de voir que
Par exemple : (6, 4) = 56 et
Pascal écrit à Fermat qu’il éprouve quelques difficultés à utiliser les combinaisons (!) pour le problème des partis. L’obstacle est d’imaginer une notation souple et facile à utiliser. Pascal, grand styliste de la langue française, méprise quelque peu le symbolisme, préférant s’exprimer en français (ou en latin) et parvenant à communiquer avec clarté. Il ne réussit cependant pas à formuler des résultats généraux, ceux-ci ne pouvant être exprimés qu’en utilisant le calcul littéral.
Son traité Des combinaisons (rédigé en latin) n’utilise pratiquement aucun symbolisme. Il est introduit par le traité Usage du Triangle arithmétique pour les combinaisons (rédigé en français, le texte latin étant placé en introduction du traité Des combinaisons). Le mot « combinaison » est défini : « Lorsque de plusieurs choses on donne le choix d’un certain nombre, toutes les manières d’en prendre autant qu’il est permis entre toutes qui sont présentées, s’appellent ici les différentes combinaisons. » Par exemple, avec les quatre lettres A, B, C et D on construit AB, AC, AD, BC, BD, CD (et Pascal insiste : « Ainsi on trouvera, par expérience… »). L’ordre n’importe pas : AB est identique à BA, et on ne retient pas AA.
Le fameux triangle arithmétique n’a pas été découvert par Blaise Pascal. Toutefois, le Clermontois a écrit le premier traité systématique sur cet objet mathématique, inventant en substance le raisonnement par récurrence, étudiant certaines applications, en particulier en « géométrie du hasard ». N’utilisant pas un symbolisme adapté, il ne parvient pas à démontrer des résultats généraux (par exemple la formule du binôme de Newton), se contentant, comme plus tard avec le traité de la roulette, de suggérer certaines conséquences importantes.
Le cas de la proposition 12
Voici comment l’hérédité de la démonstration de la proposition 12 est traitée par Pascal sur un exemple.
« Il faut donc seulement démontrer le second lemme, en cette sorte. Si cette proportion se rencontre en une base quelconque, comme en la quatrième Dλ, c’est-à-dire si D est à B comme 1 à 3, et B à θ comme 2 à 2, et θ à λ comme 3 à 1, etc. ; je dis que la même proportion se trouvera dans la base suivante, Hμ, et que, par exemple, E est à C comme 2 à 3.
Car D est à B comme 1à 3, par l’hypothèse.
Donc est à B comme
à 3,
à B comme à 3.
De même B est à θ comme 2 à 2, par l’hypothèse.
Donc à B, comme
à 2,
Mais B à E, comme 3 à 4.
Donc, par la proportion troublée, C est à E comme 3 à 2.
Ce qu’il fallait démontrer. »

On peut transcrire en langage plus moderne ce raisonnement : D/B = 1/3 donc (D + B)/B = 4/3 = E/B ; B/θ = 2/2 ou encore θ/B = 2/2, donc (B + θ)/B = 2 = C/B. Alors (B/E) × (C/B) = (3/4) × 2 = 3/2 = C/E.
La proposition à démontrer est loin d’être évidente et ne peut être devinée par simple lecture du triangle arithmétique !
références
• Dossier « Le triangle de Pascal ».
Tangente 176, 2017.
• L'œuvre scientifique de Blaise Pascal.
Pierre Humbert, Albin Michel, 1947.
• Mathématiciens français du XVIIe siècle : Descartes, Fermat, Pascal. Sous la direction de Michel Serfati et Dominique Descotes,
Presses universitaires Blaise-Pascal, 2008.
• Tous les extraits et citations proviennent des Œuvres complètes de Blaise Pascal présentées par Louis Lafuma,
Le Seuil, 1963.