Pascal est fort en maths, c’est pourquoi ses amis l’ont surnommé « Balaise Pascal ». Il a construit un rectangle de la façon suivante. Il part d’un nombre à trois chiffres, par exemple 475. Il additionne les deux premiers chiffres et note le chiffre des unités du résultat : 4 + 7 = 11, qui donne 1. Puis il fait la même chose avec les deux derniers chiffres : 7 + 5 = 12, qui donne 2. Sur la ligne suivante, il écrit le premier chiffre obtenu à gauche (1), le deuxième chiffre obtenu à droite (2), et le chiffre des unités de la somme de ces deux chiffres au milieu (3). Il itère ensuite ce processus ligne après ligne. Toute case, y compris la première, peut comporter un 0.
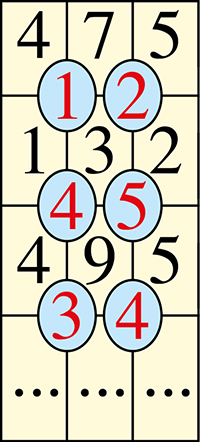
Que va-t-il se passer en poursuivant cette construction ? Le nombre d’écritures de trois chiffres étant fini, on tombera automatiquement sur une période. Quel pourra être le nombre de lignes de cette période ? En partant d’une écriture décimale x y z, observons ce qui se passe ligne après ligne.

Il faut considérer les nombres de ce tableau modulo 10 puisqu’on n’écrit que les chiffres des unités. Le chiffre des unités de 41x + 81y + 40z est le même que celui de x + y, celui de 81x + 162y + 81z est le même que celui de x + 2y + z, et celui de 40x + 81y + 41z est le même que celui de y + z. La sixième ligne du tableau sera donc identique à la deuxième : la période du rectangle de Pascal sera au plus de quatre lignes. Ce nombre est atteint avec 475 :
475 → 132 → 495 → 374 → 011 → 132…
1. Trouvez des écritures initiales de trois chiffres conduisant à des périodes de moins de quatre lignes.
Des variantes à foison
On peut imaginer de nombreuses variantes. Une première consiste à partir d’une écriture décimale à quatre chiffres xyzt. La deuxième ligne sera alors constituée des nombres x + y, x + 2y + z, y + 2z + t, z + t ; la troisième de 2x + 3y + z, 3x + 6y + 4z + t, x + 4y + 6z + 3t, y + 3z + 2t. Montrez déjà que la période est au plus de vingt-quatre lignes.
2. Expliquez pourquoi après au plus quatre lignes tous les chiffres seront pairs.
Une autre variante serait de prendre le chiffre des unités non pas de la somme mais du produit des chiffres.
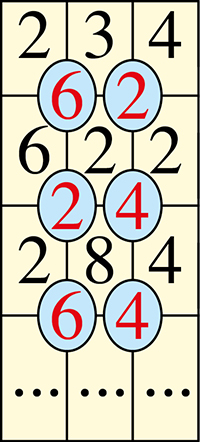
On obtiendrait ainsi la suite :
234 → 622 → 284 → 644 → 446 → 644…, avec une période de deux lignes.
3. Démontrez que la période ne peut excéder deux lignes.

