
La reconstitution par nos cerveaux de représentations 3D à partir de deux images presque identiques présentées chacune à l’un de nos yeux est connue depuis la seconde moitié du XIXe siècle. Les stéréogrammes de l’époque (constitués d’images doubles, voir article « La télévision 3D : la télé de demain ? ») s’obtenaient à partir d’appareils photographiques présentant deux objectifs dont l’écartement correspondait à celui de nos yeux (6 à 7 cm). Un système optique élémentaire (stéréoscope) permettait ensuite de visionner les clichés doubles et de retrouver la sensation du relief. C’est la technique mise en pratique aujourd’hui encore par les View-Masters de nos enfants depuis plus d’un demi-siècle, ou celle de nos téléviseurs lorsqu’ils visionnent des Blue-Rays dits 3D.
Dans tous ces cas, l’illusion du relief nécessite le recours à un truchement (lunettes ou stéréoscope). L’idée à la base de la construction des autostéréogrammes est de parvenir à recréer l’illusion du relief sans le recours à aucun intermédiaire, ce qui constitue un véritable défi. Certes, chacun de nous est capable de voir naturellement en relief (sauf handicap particulier). Mais découvrir la magie des autostéréogrammes demande un véritable apprentissage, bientôt récompensé pour certains d’entre nous (pas tous, hélas !) par la découverte d’effets cachés et surprenants. Cet apprentissage peut être facilité par une gamme d’astuces et de méthodes, jouant notamment avec des points de convergence ou des moyens optiques (viseur 3D, prismes, anamorphoses, utilisation de LED). Le champ des possibles de ce type d’images est immense ; il est étonnant de les voir si peu présentes dans les applications. Pourquoi en effet ne pas imaginer un environnement où des grillages, des paravents, des claustras (parois ajourées), des papiers peints intégreraient ce type d’illusion, inventant alors un tout nouveau design ludique 3D ?
Un nouveau design ludique 3D
Nous percevons naturellement la profondeur et le relief. Nos yeux s’orientent vers un même point, font la mise au point et transmettent au cerveau deux images que notre cortex visuel interprète. Il nous suffit de choisir : dans l’exemple ci-contre, on choisit soit de voir le château d’eau, soit de voir le grillage. Il nous est impossible de voir les deux plans nets à la fois.
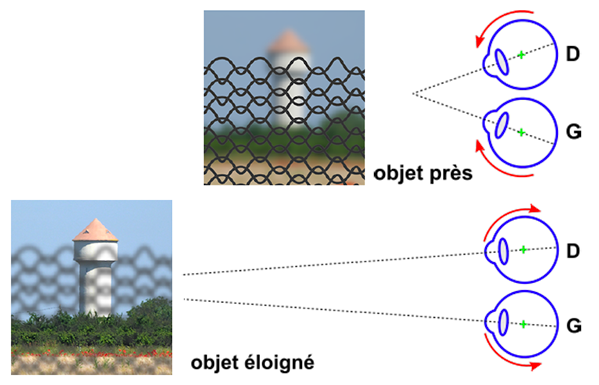
Nos yeux vont donc simultanément s’orienter vers l’objet choisi. Plus il est près, plus nos yeux louchent : c’est la convergence. Ils procèdent ensuite à la mise au point : le cristallin de chaque œil se déforme pour obtenir une vision nette. Plus l’objet est près, plus le cristallin est bombé : c’est l’accommodation. Notre cerveau reçoit et compare deux images légèrement différentes.

Plus l’objet est près, plus les images sont différentes : c’est la disparité binoculaire. Après interprétation de l’information reçue, notre cerveau nous livre une impression de volume.
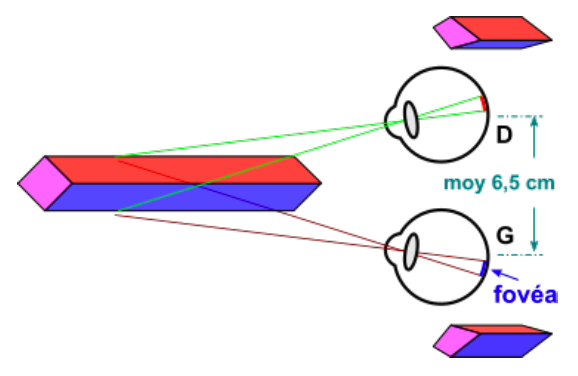
Une image plate offrant la 3D ne permet pas de respecter ces principes physiologiques car la convergence de nos yeux et l’accommodation ne se font pas sur le même plan. « Voir en 3D » nécessite donc un effort de la part de l’observateur. La vision volumique se fera aisément pour certains et plus difficilement pour d’autres. Pour d’autres encore, elle sera même impossible sans aide.
Le défi est donc d’obtenir de nos yeux qu’ils fixent un point hors de l’image sans s’accommoder sur elle. La disparité binoculaire nous demande d’utiliser soit un couple d’images stéréoscopiques, soit un autostéréogramme, que le cerveau va analyser. La convergence nous incite à fixer de nos deux yeux un point situé soit en avant (AV), soit en arrière (AR) de l’image pour amener le cerveau à faire chevaucher les modules de droite et de gauche pour les fusionner en une seule image. En fait, il existe une relation entre les distances œil–point AV–point AR–pas de l’image. Enfin, l’accommodation nous demande de laisser quelques secondes à notre appareil visuel pour corriger le dédoublement de l’image et obtenir une image nette.
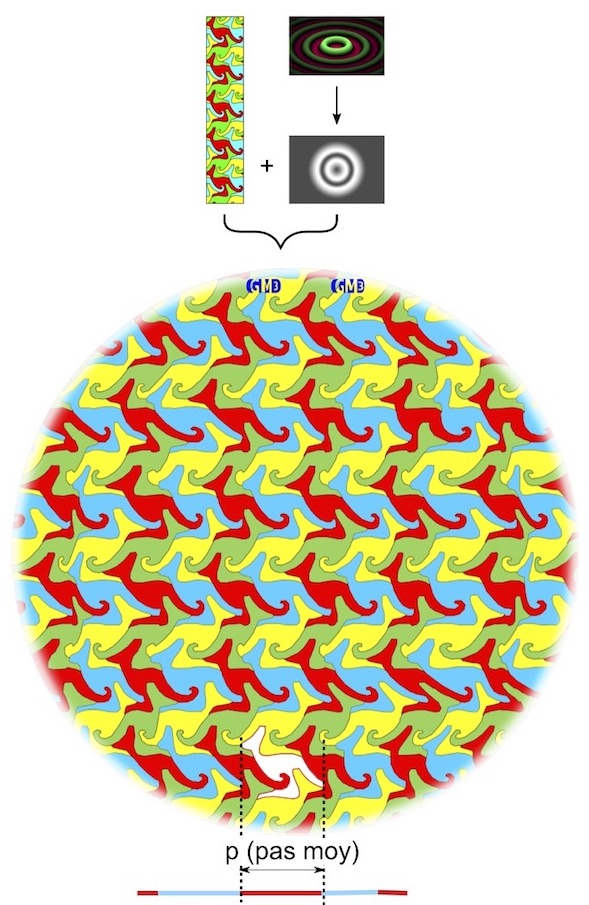
Construction d'un autostéréogramme.
Pour recréer l’illusion du relief, un autostéréogramme sera constitué d’une seule image, il est vrai, mais généralement composée à partir de la répétition horizontale d’un même motif modifié. La variation des écartements entre chaque point équivalent des motifs permet alors au cerveau de déceler le volume caché. Une grandeur significative est donc le pas de l’autostéréogramme, qui est l’écartement de deux motifs équivalents répétitifs. Dans la trame des kangourous ci-contre, le pas correspond à la largeur d’un kangourou. Le volume caché (au lecteur de le découvrir à partir de ce qui suit !) a la forme d’une onde ou d’un presse-citron en creux ou en bosse, selon la manière de le voir. Télécharger le pavage du Kangourou et son mode d'emploi.
[Le kangourou paveur utilisé pour ces images est une création de Raoul Raba, il symbolise le Kangourou des mathématiques (site Internet : www.mathkang.org). ]
Une question de convergence
Pour voir l’image stéréoscopique en 3D, nos yeux doivent converger vers un même point situé soit derrière cette image, soit devant elle pour que notre cerveau les fusionne en une seule. On peut exprimer géométriquement cette convergence par l’angle formé par deux segments partant de l’œil gauche (Og) et de l’œil droit (Od) se rejoignant en un certain point de convergence (PdC), situé en avant ou en arrière.
Pour obtenir la 3D, ces deux segments doivent obligatoirement coïncider avec le pas p du couple stéréoscopique. En vue arrière, notre œil gauche doit regarder l’image de gauche, et notre œil droit l’image de droite. Cette situation est appelée vue parallèle. En vision avant, notre œil gauche regarde l’image de droite et notre œil droit celle de gauche ; c’est la vision croisée. Ces dénominations peuvent apparaître trompeuses ; c’est pourquoi on leur préfère souvent les appellations de vue convergente en AV et vue convergente en AR. Le changement de mode de vision inverse le sens du volume, un « creux » devenant une « bosse » et réciproquement.
Trompe-l’œil et autostéréogrammes
Il s’agit de ne pas confondre les stéréogrammes avec les trompe-l’œil. Pour toutes les figures de ce type, l’artiste s’attelle à récréer l’illusion du volume à partir d’une surface plane, il s’ingénie à représenter les reliefs en utilisant tous les moyens à sa disposition, jouant de l’ombre et de la lumière, choisissant des tons généralement clairs pour l’avant-plan et nettement plus foncés (et bleutés) pour l’arrière-plan.
Rien de tout cela dans les autostéréogrammes, qui peuvent être construits, comme dans le cas des kangourous, sur base de couleurs primaires et sans aucun jeu de lumière ! Pour les trompe-l’œil, le peintre se transforme en illusionniste, comptant sur une vision « monoscopique » fondée sur une position relative bien particulière du spectateur, en sachant pertinemment que toute modification de position fera disparaître la magie de la troisième dimension.
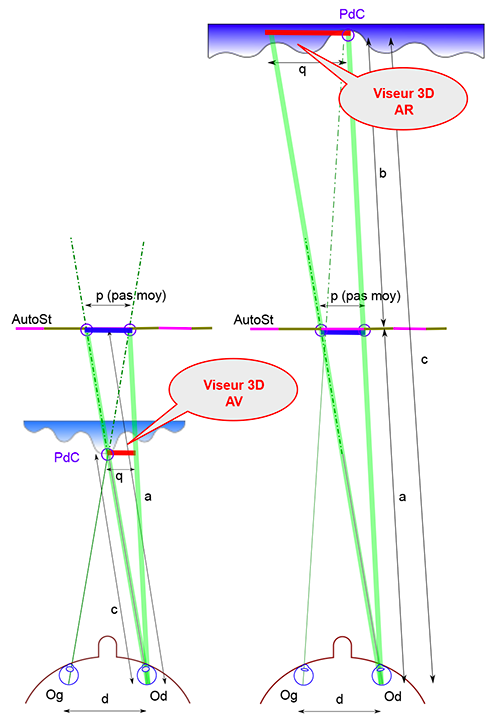
Où l’on retrouve le théorème de Thalès
Considérant que l’image stéréoscopique doit être parallèle au plan des yeux, le théorème de Thalès peut s’appliquer au triangle formé par les points Og, PdC et Od. Celui-ci nous offre alors une relation entre les données suivantes :
- L’écartement d des yeux de l’observateur, variable d’environ 6 à 7 cm selon la morphologie et l’âge des individus, avec une valeur moyenne égale approximativement à 6,5 cm ;
- Le segment p définissant le « pas moyen » de l’image et que l’on peut approcher par (pasmaxi + pasmini ) / 2, puisque ce pas est changeant dans l’image. En effet, dans le cas contraire, on aurait une simple image à motifs réguliers et donc sans effet 3D. Plus l’écart de pas est élevé, plus la profondeur sera grande ;
- La distance a entre un de nos yeux et le plan vertical de l’image ;
- La distance b entre l’image et le point de convergence PdC ;
- La distance c entre un de nos yeux et le point de convergence avec une limite physiologique inférieure dépendant de chacun de nous, et sous laquelle il est difficile de voir net (en moyenne, 25 cm).
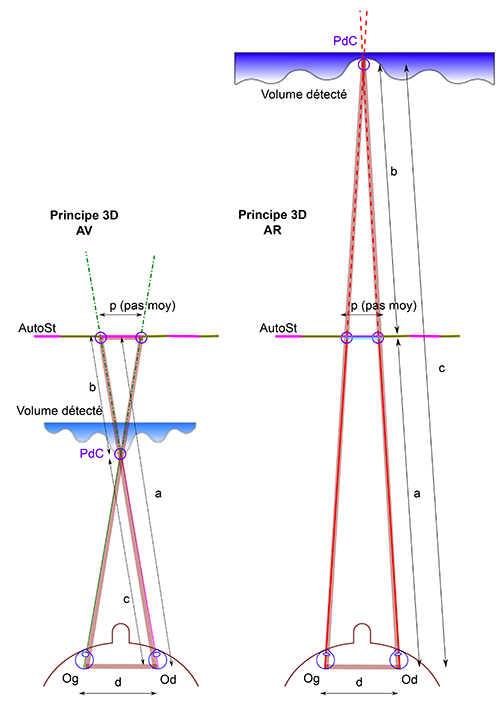
Ce que l’on recherche, c’est surtout l’apparition rapide de l’effet 3D. Il est donc préférable de se concentrer sur le centre de l’image. Dans ce cas, on peut estimer que les distances a, b et c « ne varient pas trop », quel que soit l’œil.
Imaginons à présent deux vues stéréo G–D, que l’on rapproche l’une de l’autre (le pas p diminue) jusqu’à ce qu’elles se superposent (p = 0), puis se croisent, et continuent de s’éloigner, se transformant en un couple D–G. Le passage du pas positif au pas négatif (inversion des images G et D) exprime parfaitement l’inversion du volume 3D.
Mathématiquement, les relations entre ces différentes grandeurs s’expriment selon le schéma précédent. En vue arrière, le théorème de Thalès (voir Tangente 167, 2015) nous livre :
Cette relation implique ad = cd – cp, ou encore
Notons K3D ce rapport exprimé en %. On sait que K3D > 100% puisque c > a. On en déduit que, pour une personne donnée, le rapport K3D sera directement lié au pas moyen p de l’image.
Un raisonnement identique peut évidemment être fait pour la vue arrière avec comme relation :
qui implique cette fois
Conservons ce rapport K3D en %, il permet facilement de fixer un ordre de grandeur à la position du pointeur par rapport à la distance œil–image. En vue arrière, on a c > a, et donc K3D > 100 %. En vue avant, comme c < a, on a K3D < 100 %. Ainsi, pour un observateur ayant un écart des yeux de 6,5 cm qui regarde une image située à 40 cm de lui avec un pas moyen de 3,25 cm, on calcule qu’en vision AR, on a :
K3D (en %) = d / (d – p) = 6,5 /(6,5 – 3,25) = 200 %.
Pour une image située à 40 cm de lui, il devra faire converger son regard à une distance égale à :
c = a K3D = 40 × 2/100 = 80 cm.
En vision AV, on vérifie que K3D (en %) est égal à d/(d + p), soit 6,5/(6,5 + 3,25), ou encore 67 %. Toujours pour une image située à 40 cm de lui, l’observateur devra faire converger son regard à une distance c égale à a K3D, soit 40 × 67/100, ou encore 26,6 cm.
Austères autostéréogrammes
Les calculs sont donc faits. Mais ceci n’implique nullement que nous soyons capables de situer le point de convergence d’un autostéréogramme sans l’intervention d’une calculatrice, d’une table ou d’un double décimètre. Revenons donc à notre 3D, tout en oubliant momentanément notre second œil. Il nous faut en fait déterminer quelle largeur q devrait faire un cache placé à la distance c d’un œil pour qu’il coïncide exactement avec l’angle tangent au pas p de l’autostéréogramme (situé à une distance a de l’œil). Le théorème de Thalès s’applique également à ce cas de figure.
Il faut calculer à quelle distance b placer le bâton (de hauteur h) pour s’aligner très exactement sur l’ombre de la pyramide (de hauteur H).
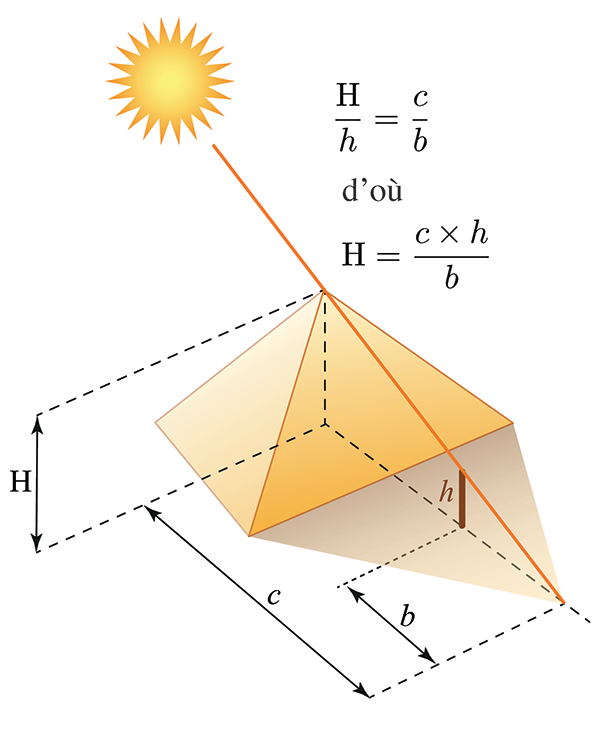
Théorème de Thalès
En vue arrière, on vérifie que
et donc
Étant donné les résultats précédents, on obtient
De manière symétrique, en vue avant, on obtient
Considérons un observateur ayant un écart des yeux de 6,5 cm qui regarde une image dotée d’un pas de 3,25 cm, située à 40 cm de lui. En vision arrière, on calcule q = 6,5 cm × 3,25 / (6,5 – 3,25) = 6,5 cm.
En vision avant, le résultat cherché devient q = 6,5 cm × 3,25 / (6,5 + 3,25) = 2,2 cm. On constate que la largeur q (le pas projeté) est directement liée au pas de l’image. Elle peut être matérialisée par un « viseur 3D » universel (sorte d’hyperbole croisée), qui permet en lecture directe d’obtenir la largeur q en abscisse pour un pas moyen lu en ordonnée.
Utilisation du viseur 3D universel
Le viseur à télécharger permet d'aider à la visualisation des autostéréogramme. Il peut être placé derrière le motif ou devant le motif. Dans ce dernier cas, il doit être imprimé sur une feuille transparante.
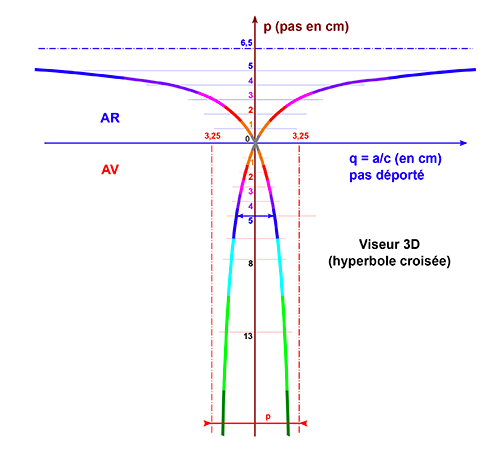
Viseur 3D universel.
1/ Pour le viseur AR : Imprimez la feuille au format A4 (100% à l'échelle1) de préférence sur papier bristol 120g ou plus si vous comptez la poser debout. il s'agit de le mettre à environ 50 cm derrière votre écran et qu'il reste visible de celui-ci (en la pliant légèrement selon l'axe vertical pour la faire tenir debout ou en la fixant sur un support). Seule la partie bleue est utilisée.
2/ Pour le viseur AV : Imprimer la feuille et reproduisez la partie rouge de la courbe (en forme d'ogive) sur une feuille transparente plutôt rigide ou un blister. Tracez ou gravez des légers traits repérant les lignes -1, -2, -3, -4, -5, -8, -13.
La représentation ci-dessous illustre les deux cas de figure (avant AV et arrière AR).
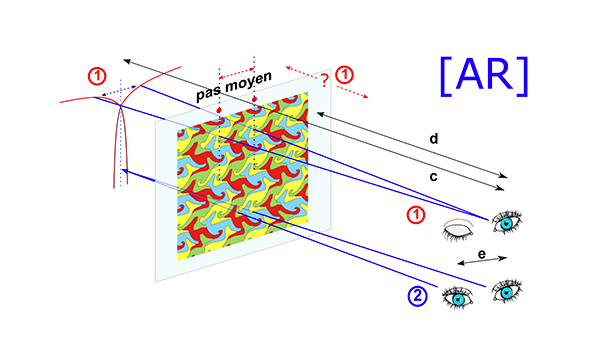
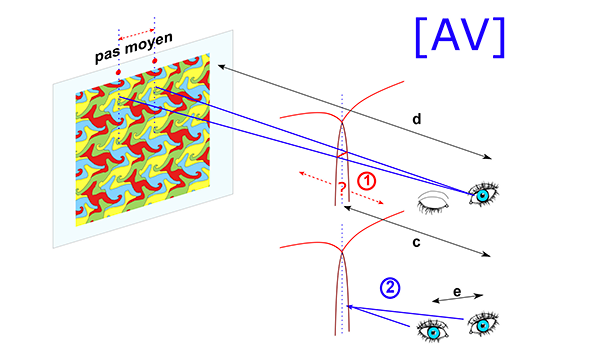
Quelles sont les perspectives de ce type d’images ? La vue arrière est limitée par l’écartement des yeux et ne permet pas d’envisager de « grandes » images (au-delà d’un mètre de large, soit seize répétitions d’un pas maximal de 6 cm). Par contre, la vue avant n’a pas cette limite, mais ce mode de vision est moins partagé.
Le viseur 3D ou la matérialisation du point de convergence dans l’installation permettrait de nouvelles applications. Un dernier conseil pour mieux déceler la 3D : choisir un environnement lumineux pour de meilleurs contrastes et orienter l’image pour obtenir un éclairage homogène, si possible sans ombre et sans effets parasites. Au lecteur de s’entraîner à présent !
Après la théorie, la pratique !
Le mur de briques paradoxal est un pliage à réaliser selon les indications à télécharger. Cet exemple montre que le cerveau peut être piégé en interprétant l'inverse du volume apparent.
Suivant la manière dont on le regarde, le ressort paradoxal peut apparaître comme une figure 3D ou une figure impossible .
Un quadrillage en relief à visualiser.
L’histoire des (auto)stéréogrammes
Le phénomène de stéréoscopie ou encore de vision binoculaire (nous avons deux yeux) a été étudié dès le début du XIXe siècle par le physicien britannique Charles Wheatstone (1802–1875), qui fut l’inventeur d’un stéréoscope à deux miroirs placés à 90°, renvoyant le regard du spectateur vers deux dessins spécialement élaborés dans le but de recréer le volume.
L’invention fut améliorée dès 1850 par le physicien écossais David Brewster (1781–1868), qui remplaça les miroirs par des lentilles. Brewster fut aussi le premier biographe d’Isaac Newton et l’auteur de l’ouvrage The stereoscope, its history, theory, and construction (1856). Il remarqua qu’en fixant le motif répétitif d’un papier peint, son cerveau avait tendance à réunir certains motifs pour créer de nouveaux objets virtuels, découvrant ainsi, sans le savoir, le principe des autostéréogrammes.
C’est au Hongrois Béla Julesz (1928–2003), qui fut longtemps directeur du Laboratory of Vision Research à la Rutgers University de Piscataway au New Jersey (États-Unis), que l’on doit une première étude exhaustive du phénomène de stéréoscopie. Le neurologue observa que lorsque des structures de points aléatoires étaient observées alternativement par chaque œil, certains de ces sous-ensembles de points semblaient appartenir à des profondeurs de champ différentes, un phénomène qu’il baptisa vision cyclopéenne.
Le neurologue Christopher Tyler, l’un des disciples de Julesz, partant toujours d’ensembles de points aléatoires, mit au point les premiers autostéréogrammes. En 1994, la sortie des ouvrages l’Œil magique (collectif, N.E. Thing Enterprises) et Stéréomagie (Jacques Ninio, Le Seuil) suscita un nouvel engouement pour le sujet.
