
Que signifie « laisser un objet inchangé » en géométrie ? Un élément de réponse semble s’imposer : « conservation des distances ». Les transformations qui conserveront un objet donné ne peuvent donc être que des isométries. Cela dit, s’il s’agit de laisser invariant un triangle quelconque, on ne trouvera guère d’autre transformation que l’identité. L’objet en question doit donc posséder un certain nombre de symétries. Pour que la recherche soit complète, il conviendra de structurer l’ensemble des isométries qui laissent invariant un même objet en y mettant une loi de composition. La merveille des merveilles sera qu’elle nous permettra de constituer un groupe.
Pour démarrer en douceur, intéressons-nous d’abord à une figure aussi élémentaire que le carré. Le cas du triangle isocèle a été traité dans l'article « Les structures quotients ».
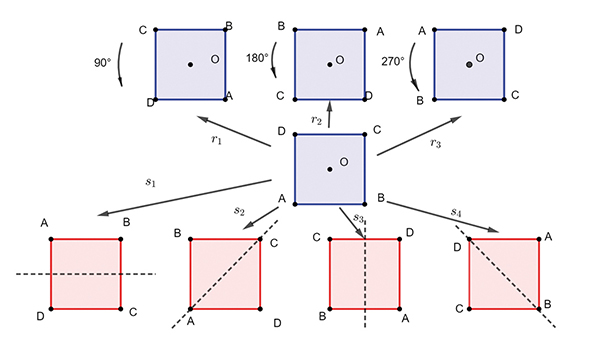
Les isométries du carré.
Un cas simple : le carré
Quels sont les isométries d’un carré ABCD ? Ce sont l’identité (Id), les rotations r1 de centre O, le centre du carré, et d’un quart de tour dans le sens trigonométrique positif, r2 = r1², r3 = r13, qui est aussi l’inverse de r1, puis les symétries s1 d’axe horizontal, s2 d’axe (AC), s3 d’axe vertical et s4 d’axe (DB).
On est en présence de D8, le groupe ... Lire la suite
