Dans la grande famille des flexagones, les tétraflexagones, de forme carrée, sont moins connus. D’un côté ils furent étudiés après les hexaflexagones par le comité flexagones (voir l'article "La petite histoire des flexagones") et en particulier par John Tukey, de l’autre ils étaient déjà découverts, pour un certain nombre d’entre eux, depuis des dizaines d’années. Mais Tukey n’arriva pas à établir une théorie générale des tétraflexagones, comme cela avait été fait pour les hexaflexagones.
Ces flexagones carrés résistent encore aux mathématiciens. Par exemple, on ne sait pas dire combien de tétraflexagones existent pour un nombre de positions stables données. De plus, leurs comportements dynamiques sont parfois assez complexes et peuvent paraître hiératiques en comparaison des cycles assez sages des hexaflexagones.
Le cycle incomplet
Le tétraflexagone le plus simple est le tritétraflexagones à 2 positions stables avec 3 couleurs. Le lecteur est fortement incité à se lancer dans sa réalisation avant de poursuivre (voir en encadré).
Construction du tritétraflexagone
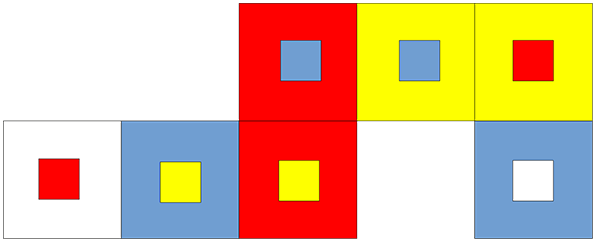
Le patron du tritétraflexagone, à reproduire, est donné ci-dessous.
La pastille dans chaque carré indique la couleur au verso.
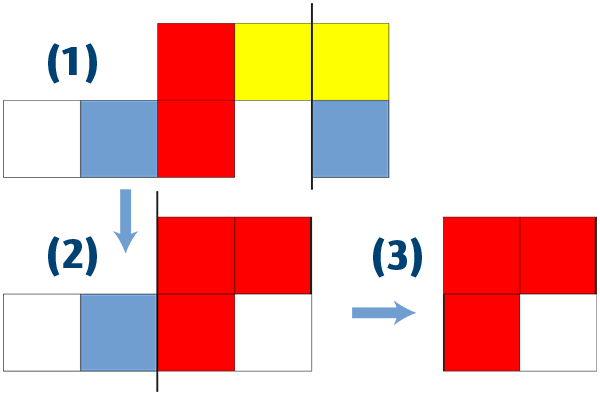
L’assemblage se fait selon le schéma suivant :