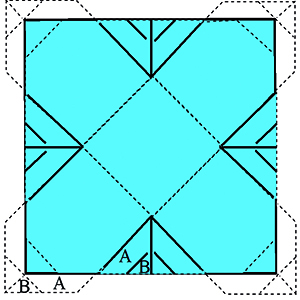
Lors de la deuxième finale du Championnat des jeux mathématiques et logiques, l’un des problèmes (supposé facile) proposait d’emballer un cube à l’aide d’un patron d’un seul tenant découpé dans une feuille de papier cadeau de 25 cm sur 60 cm, les côtés des faces devant être parallèles aux bords de la feuille de papier.
On demandait quel était alors le plus grand volume possible du cube ainsi emballé.
Les copies ont surpris les correcteurs. La réponse attendue était celle correspondant à la figure, qui entraînait une valeur égale à 123, soit 1728 cm3.
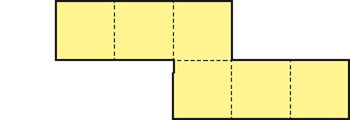
Certains participants proposèrent d’autres réponses, meilleures, avec l’un des patrons suivants. En effet, l’énoncé ne précisait pas que, sur le patron, chaque face devait être elle-même d’un seul tenant (d’où une première solution). Il ne précisait pas non plus que, pour emballer le cube, il ne devait y avoir aucun recouvrement du papier sur lui-même (d’où la seconde solution où, après découpage selon le trait plein et pliage selon les lignes pointillées, les carrés A et B doivent recouvrir la même face du cube).
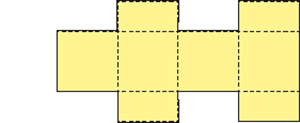
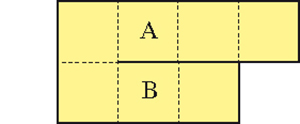
1.Dans ces deux cas, quel est alors le volume du plus grand cube possible ?
Un problème posé par Martin Gardner
Dans l’une de ses chroniques du Scientific American, Martin Gardner proposa le problème suivant : quel est le plus grand cube qui peut être complètement recouvert sur ses six faces en repliant autour de lui un gabarit d’un seul tenant découpé dans une feuille de papier carrée de côté 30 centimètres ?
Ici, on n’imposait nullement que chaque face du cube soit recouverte par une seule épaisseur de papier, ni que les côtés des faces soient parallèles aux bords du carré de papier. La réponse attendue était la suivante.

2. Si le côté du carré de papier mesure 30 cm, quel est le volume du plus grand cube qu’il est possible d’emballer complètement avec ce découpage ?
Plusieurs lecteurs proposèrent des solutions améliorant celle donnée par Gardner, mais qui nécessitaient des chevauchements de papier, ce que l’énoncé n’interdisait pas. Martin Gardner pensait qu’il n’était pas nécessaire d’interdire les chevauchements qui impliquaient une perte de surface, mais il s’est avéré que cette perte pouvait être plus que compensée en utilisant toute la surface du carré.
Dans une première solution, l’idée est la suivante. On a deux carrés qui recouvriront complètement deux faces opposées du cube. Ces deux carrés sont reliés par une bande de papier continue qui s’enroulera autour des quatre autres faces du cube. Après chaque changement de direction de la bande ou après chaque tour, il faudra faire deux petits plis où le papier sera sur deux épaisseurs, afin de continuer sur le même tour ou de se décaler pour ne pas recouvrir la bande du tour précédent.
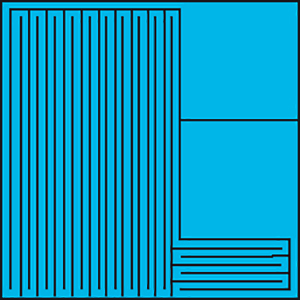
Si l’on fait tendre la largeur de la bande de papier vers 0, la somme des aires des zones où il y aura double épaisseur de papier tendra également vers zéro. On s’approche ainsi d’une limite où l’aire d’une face carrée du cube est égale au sixième de l’aire de la feuille de papier, c’est-à-dire à 900 / 6 = 150 cm2, le cube ayant alors un volume égal à (√150)3, soit 750√6 ou environ 1837 cm3.
Une autre solution proposée à Gardner a été la suivante. Le lecteur reprend le principe de la solution « officielle » du problème, mais il utilise les quatre parties blanches, qu’il découpe partiellement de façon à ce que l’ensemble reste d’un seul tenant. Ceci permet d’augmenter la taille du carré central, les parties découpées permettant, moyennant pliage, de compléter les quatre rectangles entourant le carré central et les quarts de carrés qui couvriront la face opposée à celle du carré central. En minimisant la largeur du lien entre la partie A et la plus grande partie du carré, de même qu’entre la partie B et la partie A, on minimise l’aire des recouvrements de papier. Pour faire passer la partie A de sa position initiale à sa position dans l’emballage du cube, on effectue deux plis, de même que pour juxtaposer la partie B dans sa nouvelle position.