Deux courbes fermées plongées dans l’espace forment un entrelacs. Les plus courants sont l’entrelacs trivial, composé de courbes fermées « non nouées » (donc assimilables à des cercles) telles que chacune puisse être séparée des autres sans rupture, et l’entrelacs de Hopf. Ce dernier est constitué de deux anneaux enlacés, qui ne peuvent donc être séparés sans rupture de l’un d’eux. Le mathématicien allemand Heinz Hopf (1894‒1971) fut un pionnier de la topologie algébrique.
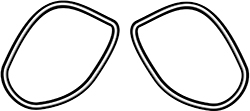
L’entrelacs trivial.

L’ entrelacs de Hopf.
Il existe des entrelacs à trois courbes ou plus tels qu’aucune des courbes qu’il contient ne puisse être séparée des autres sans rupture, mais tels que deux courbes quelconques ne soient jamais enlacées mutuellement. Le plus connu est celui des anneaux de Borromée (du nom d’une famille italienne dont les armoiries arboraient cette configuration).

Deux anneaux quelconques ne sont pas liés
et se disjoignent si l’on ôte le troisième anneau.
Il n’existe que deux configurations des anneaux de Borromée ; elles sont images-miroir l’une de l’autre. Le mathématicien allemand Hermann Brunn (1862‒1939) a beaucoup étudié ces entrelacs.

Les trois anneaux qui figurent sur les armoiries de la famille Borromée
datent du XVe siècle et symbolisent l’alliance de trois familles italiennes,
les Borromée, les Sforza et les Visconti.
Des problèmes intéressants se posent à propos des anneaux de Borromée : ces anneaux sont des courbes assimilées à des cercles. Mais ces courbes peuvent-elles être de véritables cercles de ℝ3 ? Il a été démontré que non, même si les cercles ont des rayons arbitraires ! Par contre, on a pu exhiber des configurations borroméennes de trois ou cinq carrés, de sept hexagones, de neuf octogones…
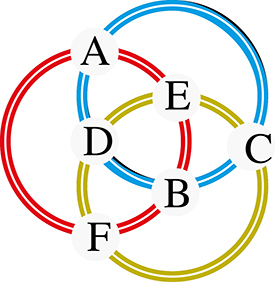
Dénombrer les configurations
Considérons trois anneaux, différenciés par leur couleur, dans la position de la figure. Il existe six croisements de deux anneaux, repérés par les lettres A à F. Pour chacun d’eux, il y a deux possibilités, selon que l’un ou l’autre passe dessus ou dessous. Au total, on a donc 26, soit soixante-quatre cas possibles.
Si aucune paire d’anneaux n’est liée, on a six cas possibles : « bleu sous jaune sous rouge », « bleu sous rouge sous jaune »… Si un anneau est lié à un deuxième et si ce deuxième anneau est lié au troisième, mais que le premier et le troisième ne sont pas liés entre eux, on obtient une chaîne de Hopf.
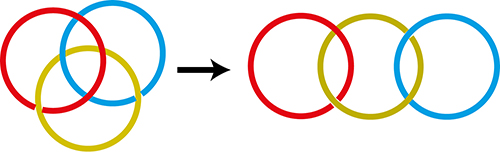
Comme le montre la figure, les anneaux rouge et bleu n’étant pas liés, on peut déplier la chaîne. Mais si on la replie, l’anneau rouge peut se glisser au-dessus ou en dessous du bleu.
1. Parmi les soixante-quatre configurations, combien existe-t-il de chaînes de Hopf ?
Une autre possibilité est que deux anneaux soient liés, et que le troisième soit « libre », c’est-à-dire qu’on puisse l’ôter sans rupture (mais dans certains cas, avec une légère déformation, en supposant que les anneaux présentent une certaine élasticité).
2. Parmi les soixante-quatre configurations, combien existe-t-il de cas où deux anneaux sont liés et le troisième libre ?
Il reste enfin le cas où les trois anneaux sont liés deux à deux. On a alors un entrelacs premier. Il existe huit configurations d’entrelacs premiers, chaque anneau pouvant être lié à un autre de deux façons.

